“জ্যামিতি আবার বোঝার কী আছে?” কিংবা “উপপাদ্য গুলো টানা মুখস্থ করে ফেলি”- দুর্ভাগ্যবশত এই ধরনের চিন্তা ভাবনা স্কুল-কলেজপড়ুয়া শিক্ষার্থীরা প্রায়ই করে থাকে। আর গণিত পরীক্ষার সময় উপপাদ্য প্রমাণ করা কিংবা সম্পাদ্যের বিদঘুটে চিত্র আঁকা অনেকের কাছেই দুঃস্বপ্নের মতন। আমি আমার পরিচিত অনেককেই দেখেছি শুধু জ্যামিতির জন্যে তারা গণিতকে ভয় পায়। কিন্তু সত্যি বলতে গণিত কিংবা জ্যামিতি কোনোটাই ভয় পাওয়ার মতো কিছু না। আর জ্যামিতি অংশে ভালো করার জন্যে তোমাকে পিথাগোরাসের মতো মহা পন্ডিত হতে হবে এমন না, বোর্ডের বই আর সামান্য ইচ্ছাই যথেষ্ট।
তাই এই ব্লগে প্রথমেই জানবো জ্যামিতি শব্দের অর্থ কি বা জ্যামিতি কাকে বলে এবং জ্যামিতি কত প্রকার? এরপর আলোচনা এগিয়ে যাবে জ্যামিতির বিভিন্ন সংজ্ঞা, জ্যামিতি সূত্র, উপপাদ্য লেখার নিয়ম এবং সম্পাদ্য লেখার নিয়ম ইত্যাদির মধ্য দিয়ে। সেই সাথে তুমি শিখতে পারবে নবম-দশম শ্রেণি ও একাদশ-দ্বাদশ শ্রেণির জ্যামিতি অংশে ভালো করার বেশ কিছু টিপস!
তাহলে চলো প্রথমেই জেনে নিই জ্যামিতি শব্দের অর্থ কি বা জ্যামিতি কাকে বলে?
জ্যামিতি কাকে বলে?
গণিতের অন্যতম একটি পুরাতন শাখা হলো জ্যামিতি, যা আমরা দৈনন্দিন জীবনে ব্যবহার করা বিভিন্ন জিনিসের আকার, কোণ, মাত্রা ইত্যাদির মধ্যে দেখতে পাই। ইংরেজি শব্দ “Geometry” -এর প্রতিশব্দ হলো জ্যামিতি। কিন্তু জ্যামিতি শব্দের অর্থ কি তা হয়ত অনেকেরই জানা নেই।
গ্রিক শব্দ geo, যার বাংলা অর্থ ভূমি এবং আরেকটি গ্রিক শব্দ metron, বাংলায় যার অর্থ পরিমাপ। এই দুটি শব্দ নিয়ে Geometry শব্দের উৎপত্তি; যার অর্থ দাঁড়ায় ভূমির পরিমাপ।
জ্যামিতি কত প্রকার?
ব্যবহার ভেদে জ্যামিতি দুই প্রকার।
১) ব্যবহারিক জ্যামিতি ও
২) তাত্ত্বিক জ্যামিতি।
ব্যবহারিক জ্যামিতি
জ্যামিতির যে শাখায় বিভিন্ন জ্যামিতি চিত্র, যেমন: বিন্দু, বস্তু, স্থান, রেখা, কোণ, ক্ষেত্র, তল ইত্যাদি আঁকার পদ্ধতি হাতে কলমে শেখা যায় তাকে ব্যবহারিক জ্যামিতি বলা হয়।
তাত্ত্বিক জ্যামিতি
জ্যামিতির যে শাখায় জ্যামিতিক উপাত্তগুলােকে সত্য প্রমাণ করা হয়, তা থেকে যুক্তি তর্ক এবং তত্ত্বের সাহায্যে নতুন কোনো সিদ্ধান্তে আসা যায় তাকে তাত্ত্বিক জ্যামিতি বলা হয়। যেমন: উপপাদ্য লেখার নিয়ম এবং সম্পাদ্য লেখার নিয়ম তাত্ত্বিক জ্যামিতির অংশ।
এছাড়া জ্যামিতির আরো কিছু প্রকারভেদ হলো-
১) বীজগাণিতিক জ্যামিতি
২) বিচ্ছিন্ন জ্যামিতি
৩) ব্যবকলনীয় জ্যামিতি
৪) ইউক্লিডীয় জ্যামিতি
৫) উত্তল জ্যামিতি
বীজগাণিতিক জ্যামিতি
বীজগাণিতিক জ্যামিতি (Algebraic Geometry) জ্যামিতির একটি শাখা, যা দিয়ে বহুমাত্রিক বহুপদীর শূন্য এবং বহুপদী বীজগণিত সমীকরণের শূন্যের সেটগুলি সমাধান করা হয়।
বিচ্ছিন্ন জ্যামিতি
জ্যামিতির যে শাখা সরল জ্যামিতিক বস্তু যেমন: বিন্দু, রেখা, ত্রিভুজ, বৃত্ত ইত্যাদির আপেক্ষিক অবস্থানের সাথে সম্পর্কিত, তাকে বিচ্ছিন্ন জ্যামিতি (Discrete geometry) বলে।
ব্যবকলনীয় জ্যামিতি
ব্যবকলনীয় জ্যামিতি বা অন্তরকলনীয় জ্যামিতি (Differential Geometry) গণিতের এমন একটি শাখা যেখানে ব্যবকলন/অন্তরকলন, সমাকলন, রৈখিক বীজগণিত ও বহুরৈখিক বীজগণিতের জ্যামিতিক সমস্যা নিয়ে আলোচনা করা হয়।
ইউক্লিডীয় জ্যামিতি
গ্রিক গণিতবিদ ইউক্লিড তার লেখা “The Elements” বইয়ে যে ধরনের গাণিতিক পদ্ধতির আলোচনা করেছেন তাই এখন ইউক্লিডীয় জ্যামিতি (Euclidean Geometry) নামে পরিচিত। কম্পিউটার বিজ্ঞান, আধুনিক গণিত সমস্যা সমাধান ইত্যাদিতে এর বিস্তৃত ব্যবহার রয়েছে।
উত্তল জ্যামিতি
উত্তল জ্যামিতি (Convex Geometry) -তে গণনামূলক জ্যামিতি, উত্তল বিশ্লেষণ, পৃথক জ্যামিতি, কার্যকরী বিশ্লেষণ, সংখ্যার জ্যামিতি, অবিচ্ছেদ্য জ্যামিতি, রৈখিক প্রোগ্রামিং, সম্ভাব্যতা তত্ত্ব ইত্যাদি নিয়ে আলোচনা করা হয়।
জ্যামিতির বিভিন্ন সংজ্ঞা
জ্যামিতি চিত্র জ্যামিতির সবচেয়ে গুরুত্বপূর্ণ ও আকর্ষণীয় অংশ। তা এবার শিখবো বেশ কিছু জ্যামিতি চিত্রসহ সংজ্ঞা –
বৃত্ত
একটি নির্দিষ্ট বিন্দুকে কেন্দ্র করে আরেকটি বিন্দু তার চারিদিকে সমান দূরত্ব বজায় রেখে একবার ঘুরে যে ক্ষেত্র তৈরি হয় তাকে বৃত্ত বলে।
বৃত্তের অন্যান্য উপাদানগুলোর জ্যামিতি চিত্রসহ সংজ্ঞা –
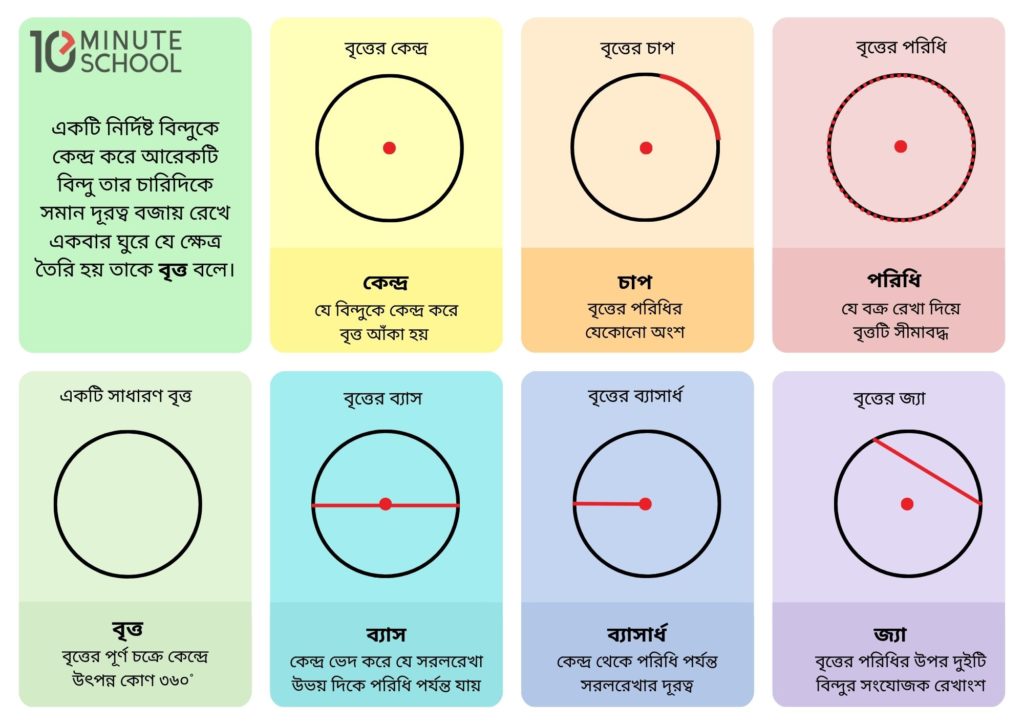
- কেন্দ্র (Center): যে বিন্দুকে কেন্দ্র করে একটি বৃত্ত আঁকা হয় তাকে ঐ বৃত্তের কেন্দ্র বলে।
- চাপ (Arc): বৃত্তের পরিধির যেকোনো অংশকে বৃত্তের চাপ বলে।
- পরিধি (Circumference): যে বক্র রেখা দ্বারা বৃত্তটি সীমাবদ্ধ হয়, তার দৈর্ঘ্যকে পরিধি বলে।
- ব্যাস (Diameter): বৃত্তের কেন্দ্র ভেদ করে যে সরলরেখা উভয় দিকে পরিধি পর্যন্ত যায় তাকে ব্যাস বলে।
- ব্যাসার্ধ (Radius): বৃত্তের কেন্দ্র থেকে পরিধি পর্যন্ত সরলরেখার দূরত্বকে ব্যাসার্ধ বলে। একই বৃত্তে একাধিক ব্যাসার্ধ আঁকা যায়।
- জ্যা (Chord): যে সরলরেখা বৃত্তের কেন্দ্র ভিন্ন পরিধির যেকোনো দুই বিন্দুকে সংযুক্ত করে তাকে জ্যা বলে। একই বৃত্তে একাধিক জ্যা আঁকা যায়।
আরো পড়ুন: শিশুর জন্য সহজ অরিগ্যামি (Origami)
ত্রিভুজ
তিনটি রেখা দ্বারা সীমাবদ্ধ ক্ষেত্রকে ত্রিভুজ বলে। ত্রিভুজ গঠিত হওয়ার পর রেখাংশ তিনটির প্রত্যেকটিকে ত্রিভুজের বাহু বলে। ত্রিভুজের তিন কোণের সমষ্টি ১৮০°।
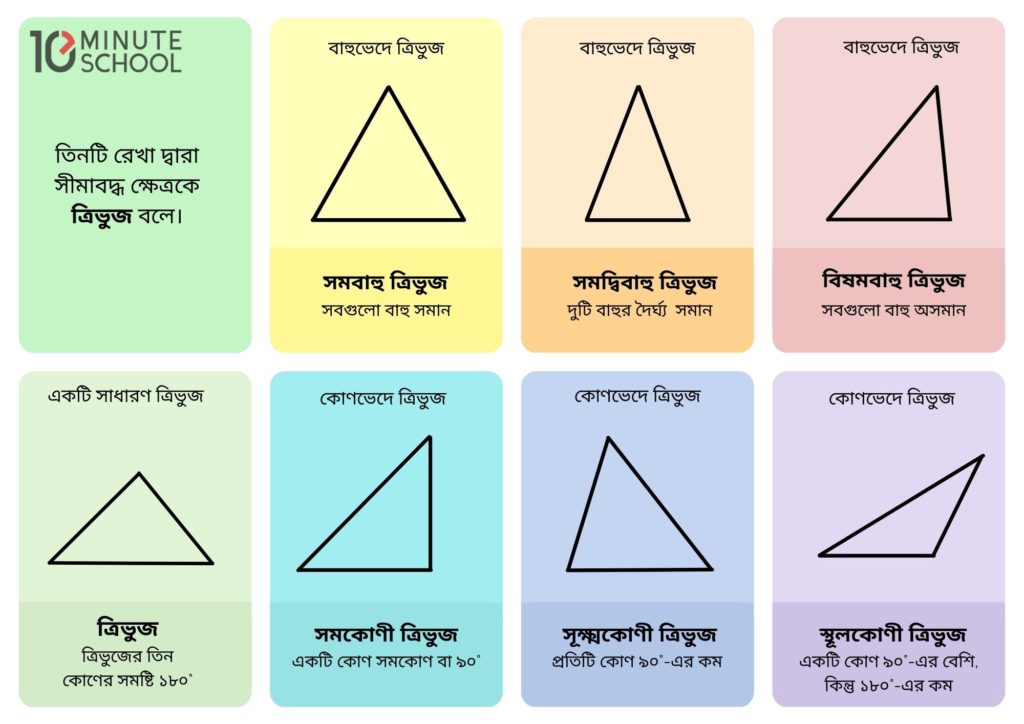
বাহুভেদে ত্রিভুজের প্রকারভেদ
বাহুভেদে ত্রিভুজ তিন প্রকার।
১) সমবাহু ত্রিভুজ (Equilateral Triangle)
২) সমদ্বিবাহু ত্রিভুজ (Isosceles Triangle)
৩) বিষমবাহু ত্রিভুজ (Scalene Triangle)
কোণভেদে ত্রিভুজের প্রকারভেদ
কোণভেদেও ত্রিভুজ তিন প্রকার।
১) সমকোণী ত্রিভুজ (Right Angle Triangle)
২) সূক্ষ্মকোণী ত্রিভুজ (Acute Angle Triangle)
৩) স্থূলকোণী ত্রিভুজ (Obtuse Angle Triangle)
চতুর্ভুজ
চারটি সরলরেখা দ্বারা সীমাবদ্ধ ক্ষেত্রকে চতুর্ভুজ বলে। চতুর্ভুজের চারটি বাহু, চারটি কোণ, অন্তর্বর্তী চারটি কোণের সমষ্টি ৩৬০°। নিচের ABCD একটি চতুর্ভুজ।
চতুর্ভুজের অন্যান্য ধরনগুলোর জ্যামিতি চিত্রসহ সংজ্ঞা –
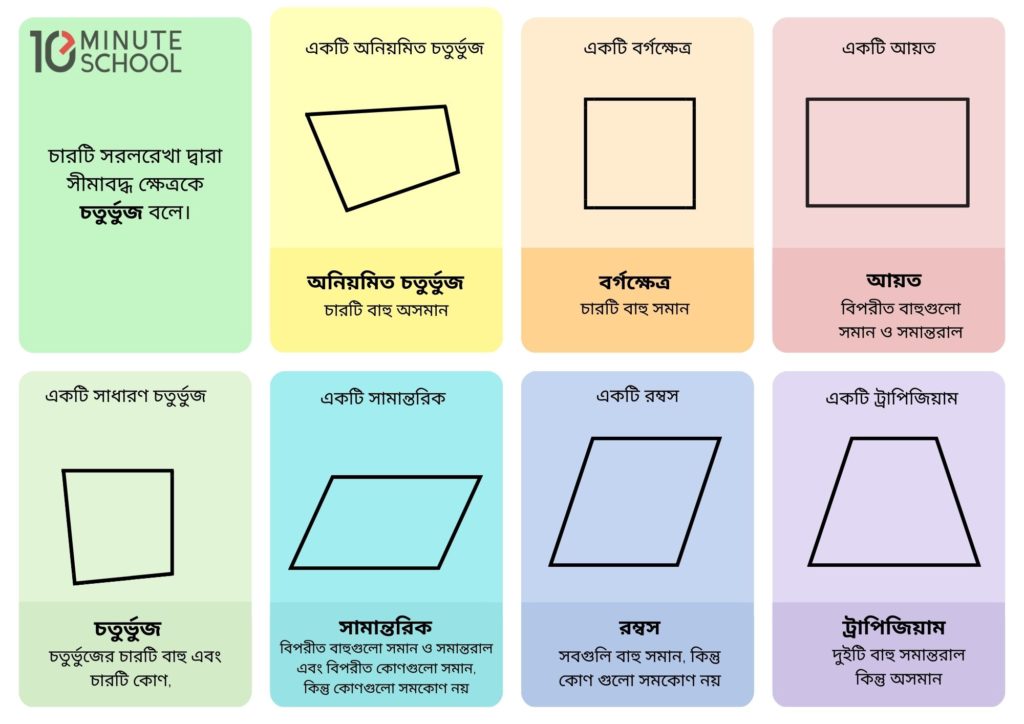
- অনিয়মিত চতুর্ভুজ: যে চতুর্ভুজের চারটি বাহুই পরস্পরের অসমান এবং কোনো সমান্তরাল বাহু নেই তাকে অনিয়মিত চতুর্ভুজ বলে।
- বর্গক্ষেত্র (Square): ৪টি সমান বাহু বা ভূজ বিশিষ্ট চতুর্ভূজকে বর্গক্ষেত্র বলা হয়, যার প্রত্যেকটি অন্তঃস্থ কোণ এক সমকোণ বা ৯০°-এর সমান।
- আয়ত (Rectangle): যে চতুর্ভুজের বিপরীত বাহুগুলো সমান ও সমান্তরাল এবং প্রতিটি কোণ সমকোণ, তাকে আয়ত বলে।
- সামান্তরিক (Parallelogram): যে চতুর্ভুজের বিপরীত বাহুগুলো সমান ও সমান্তরাল এবং বিপরীত কোণগুলো সমান (কিন্তু কোণ গুলো সমকোণ নয়), তাকে সামান্তরিক বলে।
- রম্বস (Rhombus): রম্বস এক ধরনের সামান্তরিক যার সবগুলি বাহু সমান কিন্তু কোণ গুলো সমকোণ নয়।
- ট্রাপিজিয়াম (Trapezium): যে চতুর্ভুজের দুইটি বাহু সমান্তরাল কিন্তু অসমান, তাকে ট্রাপিজিয়াম বলে।
জ্যামিতি সূত্র
গণিত মানেই এতোগুলো সূত্র! তাহলে জ্যামিতি সূত্র ছাড়া কিভাবে শেখা যায়? তাই এবার জেনে নিবো জ্যামিতি সূত্রগুলো –
বৃত্ত সংক্রান্ত জ্যামিতি সূত্র
- বৃত্তের ব্যাসার্ধের দ্বিগুণ হল ব্যাস। অর্থ্যাৎ বৃত্তের ব্যাসার্ধ = ব্যাস ÷ ২ ।
- বৃত্তের ক্ষেত্রফল = πr² = ২২/৭ × ব্যাসার্ধ × ব্যাসার্ধ।
- বৃত্তের পরিধি = 2πr
- একটি বৃত্তের পরিমাণ চার সমকোণ বা ৩৬০° ।
- একই বৃত্তের ব্যাসার্ধগুলো সমান।
- বৃত্তের একটি মাত্র কেন্দ্র থাকে।
- পরিধির ভেতরের ক্ষেত্রই বৃত্ত।
- কেন্দ্র ছাড়া বৃত্ত গঠিত হতে পারে না।
ত্রিভূজ সংক্রান্ত জ্যামিতি সূত্র
- সাধারণ ত্রিভূজের ক্ষেত্রফল = ১/২ × ভূমি উচ্চতা
- সমকোণী ত্রিভূজের ক্ষেত্রফল = ১/২ × সমকোণ সংলগ্ন বাহুদ্বয়ের গুণফল
- সমদ্বিবাহু ত্রিভূজের ক্ষেত্রফল = a/4√(4b²-a²) [যেখানে, a = ভূমি; b = অপর বাহু]
- সমবাহু ত্রিভূজের ক্ষেত্রফল = √(3/4)a² [যেখানে, a = যে কোনো বাহুর দৈর্ঘ্য]
- সমকোণী ত্রিভুজের পরিসীমা = (ভুমি + উচ্চতা + অতিভূজ)
- সমকোণী ত্রিভুজের ক্ষেত্রফল = (ভূমি × উচ্চতা) ÷ ২
- অতিভূজ² = (ভূমি² + উচ্চতা²)
- সমবাহু ত্রিভুজের পরিসীমা = 3x [যেখানে, x বাহু]
- সমদ্বিবাহু ত্রিভুজের পরিসীমা = ভুমি + সমান বাহু দুটির সমষ্টি
- বিষমবাহু ত্রিভুজের পরিসীমা = তিনটি বাহুর দৈর্ঘ্যের সমষ্টি
চতুর্ভুজ সংক্রান্ত জ্যামিতি সূত্র
- আয়তক্ষেত্রের ক্ষেত্রফল = দৈর্ঘ্য × প্রস্থ
- বর্গক্ষেত্রের ক্ষেত্রফল = বাহু²
- আয়তক্ষেত্রের পরিসীমা = ২ (দৈর্ঘ্য + প্রস্থ)
- বর্গক্ষেত্রের পরিসীমা = 4 × এক বাহুর পরিমাণ
- সামন্তরিক ক্ষেত্রের ক্ষেত্রফল = ভূমি × উচ্চতা
- ট্রাপিজিয়াম এর ক্ষেত্রফল = (সমান্তরাল বাহুদ্বয়ের সমষ্টি) × উচ্চতা
উপপাদ্য লেখার নিয়ম
জ্যামিতির একটি গুরুত্বপূর্ণ অংশ উপপাদ্য। কিন্তু বেশির ভাগ শিক্ষার্থীরাই না বুঝে উপপাদ্য লেখার নিয়ম মুখস্ত করে ফেলে। পরে দেখা যায় পরীক্ষার প্রশ্ন একটু ঘুরিয়ে প্রশ্ন হলে তারা আর পারে না। তাই এবার আমরা শিখব ধাপে ধাপে উপপাদ্য লেখার নিয়ম-
সাধারণ নির্বচন
- সাধারণ নির্বাচন লেখার মধ্য দিয়ে উপপাদ্য লেখা শুরু করতে হবে।
- এক্ষেত্রে ‘সাধারণ’ বানানের দিকে সতর্ক থাকতে হবে। সাধারণ লিখতে ‘ণ’ ব্যবহার করতে হবে, ‘ন’ ব্যবহার করা যাবে না।
- সেই সাথে ‘নির্বচন’ লিখতে হবে, নির্বাচন লিখলে ভুল হয়ে যাবে।
চিত্র
- জ্যামিতি চিত্র অবশ্যই পেন্সিল দিয়ে আঁকতে হবে, কলম ব্যবহার এবং চিত্রের গায়ে একধিক বার দাগ দেওয়া যাবে না।
- চিত্রের নামকরণ ইংরেজি বড় অক্ষরে লিখতে হবে, ছোট অক্ষরে নামকরণ করা যাবে না।
বিশেষ নির্বচন
- বিশেষ নির্বচন লেখার আগে চিত্র আঁকতে হবে, বিশেষ নির্বচনের পরে চিত্র দেওয়া যাবে না।
- বিশেষ ‘নির্বচন’ লেখতে গিয়ে ‘নির্বাচন’ লিখা যাবে না।
- বিশেষ নির্বচনে অবশ্যই চিত্রের বর্ণনা দিতে হবে।
প্রমাণ
- ‘প্রমাণ’ বানানের দিকে সতর্ক থাকতে হবে। প্রমাণ লিখতে ‘ণ’ ব্যবহার করতে হবে, ‘ন’ ব্যবহার করা যাবে না।
- প্রমাণে সমীকরণ ব্যবহার করলে, সমীকরণের নাম্বার রমার সংখ্যায় (i), (ii), (iii) ….. ব্যবহার করতে হবে।
- প্রশ্নে প্রমাণ করতে বললে প্রমাণ শেষে [প্রমাণিত] লিখতে হবে, আর দেখাও বললে প্রমান করার শেষে [দেখানো হলো] লিখতে হবে।
সম্পাদ্য লেখার নিয়ম
সম্পাদ্য লেখার নিয়ম বলতে একটি সম্পাদ্য প্রথম থেকে শেষ পর্যন্ত লিখার ধাপগুলোকে বুঝায়। তাই এবার আমরা ধাপে ধাপে সম্পাদ্য লেখার নিয়ম শিখবো –
সাধারণ নির্বচন
- উপপাদ্যের সম্পাদ্যও সাধারণ নির্বাচন লেখার মধ্য দিয়ে লেখা শুরু হয়।
- সাধারণ নির্বচন অংশে সম্পাদ্যের জ্যামিতিকে সরলভাবে ব্যাখ্যা করা হয়।
চিত্র অংকন
- সম্পাদ্যে চিত্র অবশ্যই পেন্সিল দিয়ে আঁকতে হবে, কলম ব্যবহার এবং চিত্রের গায়ে একধিক বার দাগ দেওয়া যাবে না।
- সম্পাদ্যের চিত্রে নির্দেশিত জ্যামিতিক আকৃতি চিহ্নিত করে দেখাতে হবে।
বিশেষ নির্বচন
সম্পাদ্যের বিশেষ নির্বচন অংশে সম্পাদ্যের তথ্য বা উপাত্ত কে বর্ণনা করতে হবে।
অংকনের বিবরণ
সম্পাদ্যে অংকনের বিবরণ লিখার ক্ষেত্রে এই ধারাবাহিকতা অবশ্যই রক্ষা করতে হবে। অংকনের বিবরণ লেখার সময় ধারাবাহিকতা অনুসরণ খুবই গুরুত্বপূর্ণ। অংকনের বিবরণের ধারাবাহিকতা বলতে বোঝায় যে কাজটি আগে করা হয়েছে তা আগে লিখতে হয় এবং যে কাজটি পরে হয়েছে তা পরে লিখতে হয়।
প্রমাণ
সম্পাদ্যের এ অংশে যুক্তি দ্বারা অঙ্কিত চিত্রের নির্ভুলতা প্রমাণ করে [প্রমাণিত] লিখতে হবে।
মাধ্যমিক এবং উচ্চ মাধ্যমিক উভয় ক্ষেত্রে জ্যামিতি পাঠ্যক্রমে থাকলেও তাদের ধরন আসলে ভিন্ন রকম। মাধ্যমিক স্তরের জ্যামিতি যেখানে উপপাদ্য, সম্পাদ্য অথবা পরিমিতির অংকের মাঝে সীমাবদ্ধ সেখানে উচ্চমাধ্যমিক স্তরের জ্যামিতি আরও বেশি প্রয়োগমূলক এবং স্থানাংক ভিত্তিক। তাই মাধ্যমিক এবং উচ্চমাধ্যমিক শিক্ষার্থীদের জ্যামিতি অংশের ভীতি কাটানোর জন্যে আলাদা করে পরামর্শ উপস্থাপন করছি।
জ্যামিতি টিপস (নবম-দশম শ্রেণি)
১) আকৃতিগুলোর সম্পর্কে মৌলিক ধারণা বৃদ্ধি করো
তুমি যদি একটু খেয়াল করে দেখো, তোমার পাঠ্যবইয়ের জ্যামিতি অংশের সব কথাবার্তা কিন্তু ত্রিভুজ, চতুর্ভুজ, বৃত্তের সাথে অন্যান্য কিছু পরিচিত আকৃতি নিয়েই। কিন্তু খুব দুঃখের বিষয় আমরা এই আকৃতিগুলোর সংজ্ঞা, প্রকারভেদ এবং বৈশিষ্ট্যগুলো সম্পর্কে খুব বেশি না জেনেই বড় উপপাদ্য প্রমাণের কাজে লেগে পড়ি। অনেকেই প্রশ্ন করে বসতে পারো, “এগুলো জেনে কী হবে? পরীক্ষায় তো সরাসরি সংজ্ঞা, প্রকারভেদ কিংবা জিজ্ঞেস করা হয় না।”
এই প্রশ্নের উত্তরে একটা উদাহরণ দেয়া যাক, যদি তুমি একটা দেয়াল তৈরি করতে চাও তাহলে তোমার ইট, বালি,সিমেন্টের প্রয়োজন হবে। আবার যদি একটা দালান বানাতে চাও, তাহলে অনেকগুলো দেয়াল, পিলার, ছাদ দিয়েই তৈরি হবে দালান। একটা উপপাদ্য প্রমাণ করা কোনো অংশেই দেয়াল কিংবা দালান তৈরির থেকে কম না। আকৃতিগুলোর সংজ্ঞা, বৈশিষ্ট্য এবং ধর্ম দিয়েই ধাপে ধাপে প্রমাণ করা হবে একটা উপপাদ্য। তাই এইসব আকৃতিগুলো সম্পর্কে মৌলিক ধারণা রাখা অত্যন্ত জরুরি। মৌলিক বিষয়গুলোর কিছু উদাহরণ হলো:
- ত্রিভুজের তিন কোণের সমষ্টি ১৮০ ডিগ্রী।
- চতুর্ভুজের চার কোণের সমষ্টি ৩৬০ ডিগ্রী।
- ত্রিভুজের একটি বাহুকে বর্ধিত করলে যে বহিঃস্থ কোণ উৎপন্ন হয়, তা এর বিপরীত অন্তঃস্থ কোণদ্বয়ের সমষ্টির সমান।
- ত্রিভুজের একটি বাহুকে বর্ধিত করলে যে বহিঃস্থ কোণ উৎপন্ন হয়, তা এর বিপরীত অন্তঃস্থ কোণ দু’টির প্রত্যেকটির থেকে বড়।
- সমকোণী ত্রিভুজের সূক্ষকোণদ্বয় পরস্পর পূরক।
- বৃত্তে অন্তর্লিখিত সামান্তরিক একটি আয়তক্ষেত্র।
- বৃত্তের কোনো বিন্দুতে একটিমাত্র স্পর্শক আঁকা সম্ভব।
- বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে ঐ বৃত্তে কেবল দুইটি স্পর্শক আঁকা যায়।
তোমাদের পাঠ্যবই থেকেই উদাহরণগুলো সংগ্রহ করেছি। আর এমন সব মৌলিক বিষয়গুলো জানতে পাঠ্যবইয়ের অনুশীলনীর আগে লেখা কথাবার্তাগুলো পড়ো বেশি বেশি।
২) কোণের সম্পর্কে ধারণা বাড়াও
বইয়ের পাতায় বিদঘুটে সম্পাদ্যের চিত্রের নিচে যে “অংকনের বিবরণ” লেখা থাকে সেখানে মাঝে মাঝেই দেখবে হঠাৎ সূক্ষ্মকোণ কিংবা স্থূলকোণ আঁকা হয়। আবার উপপাদ্যের প্রমাণেও দেখা যায় “তারা পরস্পর বিপ্রতীপ কোণ” কিংবা “তারা পরস্পর সম্পূরক কোণ”-এই ধরনের লেখা। এখন তুমি যদি সূক্ষ্মকোণ আর স্থূলকোণ কীভাবে আঁকতে হয় তা না জানো অথবা বিপ্রতীপ কোণ আর সম্পূরক কোণ কখন হয় তা না জানো, তাহলে তোমার জন্যে সম্পাদ্য আঁকা কিংবা উপপাদ্য প্রমাণ করা উভয়ই প্রায় অসম্ভব হয়ে যাবে। আকৃতির মতন কোণ সম্পর্কেও বিস্তারিত ধারণা থাকা চাই।
সন্নিহিত কোণ, সমকোণ, স্থূলকোণ, সূক্ষ্মকোণ, প্রবৃদ্ধ কোণ, সরল কোণ, সম্পূরক কোণ, পূরক কোণ, বিপ্রতীপ কোণ ইত্যাদি গুরুত্বপূর্ণ কোণ সহ সকল কোণ সম্পর্কে মৌলিক ধারণা নেওয়া এবং তাদেরকে আঁকতে শেখা উপপাদ্য প্রমাণ কিংবা সম্পাদ্য আঁকার জন্যে অত্যন্ত জরুরি। পাঠ্যবইয়ের পাতায় পেয়ে যাবে তাদের সম্পর্কে বিস্তারিত সব তথ্য।
৩) কঠিন টার্মগুলো সম্পর্কে জানো
সত্যি কথা বলতে বইয়ের পাতায় উপপাদ্যের প্রমাণ কিংবা সম্পাদ্যের অংকনের বিবরণ অনেক কঠিন ভাষাতে উপস্থাপন করা হয়। তার সাথে জ্যামিতির কিছু কিছু কঠিন টার্ম বিষয়টাকে আরও বেশি ভীতিকর বানিয়ে ফেলে। কিন্তু এই কঠিন শব্দগুলোর অর্থ বোঝার চেষ্টা করলে আসলে সম্পূর্ণ বিষয়টাকে সহজেই আয়ত্বে আনা যায়।
যেমন ধরা যাক সর্বসমতা। দুইটি ত্রিভুজ কখন সর্বসম হয়? যখন দুইটি ত্রিভুজের তিন কোণ এবং তিন বাহু পরস্পরের সমান হয় তখন বলা হয় ত্রিভুজ দুইটি সর্বসম। এই রকম অসংখ্য টার্ম জ্যামিতিতে ব্যবহার করা হয়। আগে থেকেই এ সকল টার্ম সম্পর্কে ধারণা থাকলে উপপাদ্য প্রমাণে সমস্যা হওয়ার কোনো সুযোগ নেই।
সম্পাদ্য আঁকার ক্ষেত্রেও বেশ কিছু টার্ম থাকে। যেমন, বাহুর সমদ্বিখণ্ডক কিংবা কোণের সমদ্বিখণ্ডক, বৃত্তের ক্ষেত্রে বৃত্তচাপ নেয়া, কম্পাসের সাহায্যে লম্ব আঁকা ইত্যাদি ছোটখাটো বিষয়গুলো আগে থেকে দেখে রাখলে সম্পাদ্য আকাঁর সময় আটকে যাওয়ার সম্ভাবনা কমে যাবে।
৬ষ্ঠ থেকে ১০ম শ্রেণি অনলাইন ব্যাচ ২০২৪
ফুল সিলেবাস কোর্সে যা যা থাকছে:
৪) মুখস্থকে না বলো
শুরুতেই বলেছি, জ্যামিতি কিংবা গণিত কোনোটিই ভয় পাওয়ার কিংবা মুখস্থ করার বিষয় না। আমার তো মনে হয় না বইয়ের পাতায় থাকা পঞ্চাশটার বেশি উপপাদ্যের প্রমাণ এবং তার প্রায় সমপরিমাণ সম্পাদ্যের অংকনের বিবরণ কারো পক্ষে মুখস্থ করা আসলেই সম্ভব। এই গুরুগম্ভীর লেখাতেও তোমাদের একটা চমৎকার ঘটনা বলি যা তোমাদের মুখস্থ না করার উপকার সম্পর্কে ধারণা বাড়াবে।
স্কুলে আমার বেশকিছু গণিতপ্রেমি বন্ধু ছিলো যারা কিনা গণিত মুখস্থ না করে মৌলিক বিষয় গুলোকে বোঝার এবং নিজের আয়ত্বে আনার চেষ্টা করতো সবসময়। তাদের সব থেকে অসাধারণ কাজ ছিলো বইয়ের উপপাদ্যগুলো কীভাবে ভিন্ন এবং যুক্তিসংগতভাবে প্রমাণ করা যায়। একবার পরীক্ষার হলে তাদের মধ্যে একজন একটা বড় উপপাদ্যকে খুব অল্প কথায় যুক্তি দিয়ে প্রমাণ করে। কিন্তু শিক্ষক প্রথমে তাকে কোনো নম্বর দেননি। পরবর্তীতে শিক্ষকের কাছে আপিল করলে তিনি অবাক হয়ে তাকে পূর্ণ নম্বর দিয়েছিলেন। মুখস্থ না করে জ্যামিতির মৌলিক ধারণা বৃদ্ধি করার মাধ্যমেই জ্যামিতিতে ভালো করা সম্ভব।
যখন তুমি উপপাদ্যের পেছনের কথাগুলো সম্পর্কে জানবে তখন তোমার কাছে তা প্রমাণ করা খুব কষ্টের কিছু মনে হবে না। তখন দেখবে একটু চেষ্টা করলেই তা প্রমাণ করা যাচ্ছে মুখস্থ করার কোনো প্রয়োজনই পড়ছে না।
৫) পরিমিতি ও ঘন জ্যামিতির ক্ষেত্রে করণীয়
পরিমিতি ও ঘন জ্যামিতি অনেকটাই প্রমাণ এবং অঙ্কন ভিত্তিক জ্যামিতি থেকে আলাদা। এখানে ত্রিভুজ, চতুর্ভুজ,বৃত্ত এসব আকৃতি তার সাথে বিভিন্ন ত্রিমাত্রিক আকৃতি যেমন, সিলিন্ডার, গোলক, প্রিজম ইত্যাদি দিয়েই ক্ষেত্রফল, আয়তন, পৃষ্ঠতলের ক্ষেত্রফল ইত্যাদি নির্ণয় করা হয়।
সবার আগে সূত্রগুলোর প্রমাণসহ ভালোভাবে বোঝার চেষ্টা করে নিজের আয়ত্বে আনতে হবে। কীভাবে সূত্রগুলো প্রয়োগ করতে হয় তা শিখে নিতে হবে, তার সাথে বিভিন্ন টাইপ ভিত্তিক অংক বই থেকে প্র্যাক্টিস করে যেতে হবে। তাহলেই পরিমিতি এবং ঘন জ্যামিতি অংশে ভালো করা সম্ভব।
জ্যামিতি টিপস (একাদশ-দ্বাদশ শ্রেণি)
১) স্থানাংক ব্যবস্থা সম্পর্কে মৌলিক ধারণা বাড়ানো
মাধ্যমিক স্তরের ত্রিভুজ, চতুর্ভুজ, বৃত্ত নিয়েই উচ্চ মাধ্যমিকে কাজ করা হয় কিন্তু ভিন্ন ভাবে৷ এখানে উপপাদ্য প্রমাণ কিংবা সম্পাদ্য অংকনের প্রয়োজন না থাকলেও সেই পুরনো উপপাদ্যগুলোই ঘুরিয়ে-ফিরিয়ে কাজে আসে। কিন্তু এখানে অংক করা লাগে প্রতিটি ক্ষেত্রে এবং সকল হিসাব করা হয়ে থাকে স্থানাংক পদ্ধতিতে। তৈরি করতে হয় নানা ধরনের সমীকরণ।
সরলরেখার ক্ষেত্রে, বিভিন্ন বিন্দুগামী সরলরেখার সমীকরণ নির্নয়, সরলরেখার মধ্যমা নির্নয়, বিভিন্ন বিন্দু থেকে সরলরেখার দূরত্ব নির্ণয় ইত্যাদি এবং বৃত্তের ক্ষেত্রে, বিভিন্ন বিন্দু ও সরলরেখা স্পর্শ করে তৈরি করা বৃত্তের সমীকরণ নির্ণয় করতে হয় সাথে আরও অনেক কিছু। এই সব ক্যাল্কুলেশন মূলত করা হয় স্থানাংক ব্যবস্থার মাধ্যমে। বিভিন্ন বিন্দু এবং চতুর্ভাগের হিসাব করার ধারণা বৃদ্ধি করতে হবে।
২) থিওরিতে গুরুত্ব প্রদান করা
উচ্চমাধ্যমিকের ক্ষেত্রে জ্যামিতি অংশে যার থিওরি সম্পর্কে ধারণা যতো পরিষ্কার থাকবে তার পক্ষে ততো বেশি ভালো করা সম্ভব। সরলরেখা, বৃত্ত, কনিক-এর গুরুত্বপূর্ণ থিওরিগুলো অনুশীলনীর অংক ধরার আগেই পড়ে নিতে হবে। সাথে সূত্রগুলোর শেকড় থেকে ডালপালা সব কিছু সম্পর্কে ধারণা রাখা প্রয়োজন। বিভিন্ন শর্ত রয়েছে যেগুলো হরহামেশাই অংক করার সময় কাজে আসে, এগুলোকে কখনোই এড়িয়ে চলা উচিত না।
৩) মোবাইল ফোনে গ্রাফিং ক্যালকুলেটর ব্যবহার
যেহেতু উচ্চমাধ্যমিক পর্যায়ে জ্যামিতিগুলোকে গ্রাফের মাধ্যমে উপস্থাপন করা হয় এবং পরীক্ষার হলেও গ্রাফের মাধ্যমেই সৃজনশীল প্রশ্ন উপস্থাপন করা হয়, তাই মোবাইল ফোনে গ্রাফিং ক্যালকুলেটর ব্যবহার করা হতে পারে একটি অসাধারণ সমাধান! DESMOS নামে একটি ফ্রী গ্রাফিং ক্যালকুলেটর গুগল প্লে স্টোরে পাওয়া যায় যা অসম্ভব কার্যকর উচ্চ মাধ্যমিক পর্যায়ে জ্যামিতিতে আশানুরূপ ফল অর্জনের জন্য।
আরও পড়ুন: গণিত পরীক্ষার ভয় আর নয়
জ্যামিতি নিয়ে কিছু খুঁটিনাটি প্রশ্ন
- ১) জ্যামিতি শব্দের অর্থ কি
- উত্তর: জ্যামিতি শব্দের অর্থ ভূমির পরিমাপ।
- ২) জ্যামিতির জনক কে?
- উত্তর: গ্রিক গণিতবিদ ইউক্লিড।
- ৩) জ্যামিতির প্রথম ব্যবহার শুরু হয় কোথায়?
- উত্তর: আকৃতি ও পরিমাপ নিয়ে গণিতের অন্যতম জটিল শাখা জ্যামিতির উদ্ভব হয়েছিল প্রাচীন ব্যাবিলনে।
- ৪) কে সর্বপ্রথম জ্যামিতির মৌলিক ধারণার ভিত্তি রচনা করেন?
- উত্তর: খ্রিস্টপূর্ব ৩০০ অব্দে গ্রীক পণ্ডিত ইউক্লিড সর্বপ্রথম জ্যামিতির মৌলিক ধারণার ভিত্তি রচনা করেন ।
- ৫) আধুনিক জ্যামিতির জনক কে?
- উত্তর: গ্রিক গণিতবিদ ইউক্লিড।
শেষ কথা
সবশেষে যে কাজটা সবচেয়ে বেশি গুরুত্বপূর্ণ, তা হলো অনুশীলন। তুমি অনেক ভালো জ্যামিতি বুঝলেও অনেক দিন প্র্যাক্টিসের বাহিরে থাকলে আসলে তোমার টার্মগুলোর সাথে মানিয়ে নিতে সমস্যা হবে। অন্যদিকে তুমি যদি খুব ভালো জ্যামিতি নাও পারো, প্রতিদিন চেষ্টা করতে করতেই একটা ভালো পর্যায়ে নিয়ে যেতে পারবে নিজেকে। জ্যামিতি ভয় পেয়ে এড়িয়ে গেলে কিংবা বোকার মতন মুখস্থ করে দিন শেষে কোনো ফলাফল পাওয়া যাবে না। তাই চর্চা করতে থাকো, নিজেই বুঝে যাবে জ্যামিতি জিনিসটা আসলেই কতো মজার!
১০ মিনিট স্কুলের অনলাইন ব্যাচগুলোতে ভর্তি হতে ক্লিক করো:
- ৬ষ্ঠ-১০ম শ্রেণির পড়াশোনার সবকিছু নিয়ে টেন মিনিট স্কুল অনলাইন ব্যাচ!
- ৯ম শ্রেণি অনলাইন ব্যাচ ২০২৩ [বিজ্ঞান বিভাগ]
- ১০ম শ্রেণি [SSC 2024] অনলাইন ব্যাচ [বিজ্ঞান বিভাগ]
- SSC 2023 শেষ মুহূর্তের প্রস্তুতি কোর্স [বিজ্ঞান বিভাগ]
- HSC 2023 শর্ট সিলেবাস ক্র্যাশ কোর্স [বিজ্ঞান বিভাগ]
- HSC 2024 ক্র্যাশ কোর্স – প্রথম পত্র [বিজ্ঞান বিভাগ]
আপনার কমেন্ট লিখুন